March 28, 2020

Recreating Bitcoin 5:Public Key and Private Key

Public Key & Private Key #

So how are the public key and private key of a user generated?

This is precisely the essence of asymmetrical encryption. User’s public key is derived from private key through computation, and user’s private key is counter-intuitively generated by the user themselves.

How is a private key generated?

Private key and public key in essence are numbers. If we treat any number as a private key, we can use elliptical curve cryptography to generate the corresponding public key of this number. That is, Function elliptical curve encryption (private key) = public key.

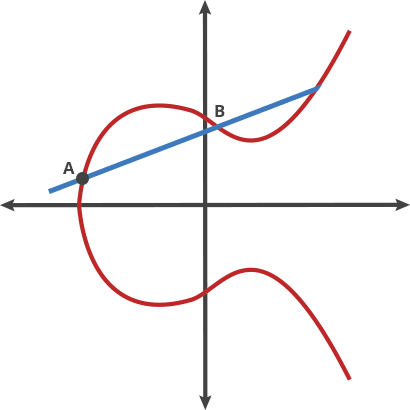
elliptical curve cryptography

If we let the user to randomly generate numbers and make the range of possibilities large enough, we can prevent two users from generating the same private key - that is, conflict of private key.

But then How large is large enough?

The answer is two to the power of 256.

The essence of creating private key is obtaining a number between 1 and 2 to the power of 256.

One way you could do it is by throwing a coin 256 times and record each result, which would look something like this:

11111001011100
1100100010011010
10101010110011110
00011010000000
0000000000000
0000000000000
0000000000000
0000000000000
0000000000000
0000000000000
0000000000000
0000000000000
0000000000000
0000000000000
0000000000000
0000000000000
0000000000000
0000000000000
0000000000000

That’s a total of 256 binary characters. We can transform it into that of a hexadecimal order to reduce it to a total of 64 characters, each representing 4 bits.

(Note: one binary number represents 1 bit. 1-bit information is what makes
a 50% probability into 100% certainty. The energy of the information of that size is 1 bit. For example: in the binary system, the number can only be either 0 or 1, each representing a 50% chance. If 1 is produced, then the 50% uncertainty has been turned into a 100% certainty, representing 1 bit. Vice versa for the case of 0. Either represents the energy of 1 bit. The information needed to produce this kind of certainty is 1 bit.)

In the hexadecimal order, the result looks like this:

f97c89aaacf0cd2e47ddba
cc97dae1f88bec49106ac3
7716c451dcdd008a4b62

The public key, which calculated using the private key, would also be in hexadecimal order:

b4327ae841ca6cfd1203cc
6e135a48d893cbfb2c388
c0f64a79694199cc9b4cb

We can further transform it into based-64 for a shorter representation:

1BJhat1AMGYbT9HYJxVek
oCaPaqB9ZyTyF

Base-2: each character has the options of 0-1, two possibilities.

Base-16: each character has the options of 0-15, 16 possibilities, consisted of 0-9 and A-F.

Base-64: each character has the options of 0-63, 64 possibilities, almost taking up all the keys on a standard keyboard.

Theoretically, if we can invent a keyboard with keys that contain special characters such as stars and triangles, we could potentially have 128 characters in total, enough to implement base-128. But so far the global standard only includes slightly more than 64 characters, so base-64 is what we use.

(Note: The real world Bitcoin system uses base-58, a modified version of base-64)

2²⁵⁶ is a number very hard to imagine. In decimal place, it is approximately 10⁷⁷ (the observable portion of the universe has about 1080 atoms). We can basically regard the chance of coincidence as 0.

Because users do not produce their private and public keys with the server, the server does not know the existence of the user in advance, which means that by getting rid of the account model, we get rid of user registration. By getting rid of user registration, the server cannot limit the user freedom.

By using public key as the recipient address, we also improve the privacy protection of the user identity (It is important to note here that the privacy of Bitcoin is protected by changing names rather than anonymity).

Bitcoin made one more step towards freedom of Transactions.

The setting sun fell through the windows of the cafe, gilding the room with a golden color.

Satoshi is still engrossed in the screen, tapping away at the keyboard.
On the side, Gilfoyle was tossing a coin over and over again on the table, recording it with a pencil.

Satoshi asked him, “What are you doing?”

Gilfoyle answered, “Making my own private key.”

“Do it with your computer. It doesn’t take a second,” Satoshi said.

“I don’t trust a computer. I only trust my coin,” Gilfoyle said.

Next chapter ：Recreating Bitcoin 6:Version 0.0.2 is Online!